IOException.de

Anscheinend war es wohl mal wieder Zeit für einen etwas theoretischeren Beitrag. Binärbäume sind in der Informatik eine wichtige Datenstruktur, mit der sich beispielsweise Rechenterme abspeichern lassen. Sie bestehen aus Knoten, die einen linken und/oder rechten Knoten besitzen können, welche selbst wieder Unterknoten besitzen können. Mehr dazu findet man unter anderem bei Wikipedia.

Binärbäume werden über rekursive Aufrufe traversiert, bei (Binär-)Bäumen gibt es hauptsächlich drei wichtige Traversierungen: Pre-Order, In-Order und Post-Order. Ein Traversierungschritt besteht jeweils aus drei Teilschritten: Auswertung des aktuellen Knotenwerts, und der rekursive Abstieg in den linken und rechten Unterknoten. Der Name gibt jeweils an, an welcher Stelle die Auswertung des aktuellen Knotens stattfindet. Bei einer Post-Order-Traversierung wird also erst, der linke und der rechte Knoten rekursiv aufgerufen, und dann erst der aktuelle Knoten selbst ausgewertet. Hier ein Beispiel:

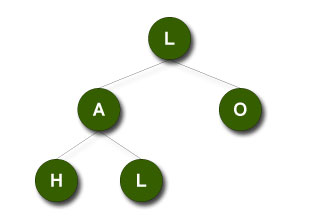
Pre-Order: L A H L O
In-Order: H A L L O
Post-Order: H L A O L
Nun ist es eine beliebte (Prüfungs-)Aufgabe, anhand zweier gegebenen Traversierungen den Originalbaum rekonstruieren zu lassen. In manchen Lehrbüchern ist zu finden, dass dies mit zwei Traversierungen möglich ist. Allerdings misslang mir dies bei einigen Versuchen mit Pre- und Post-Order-Ausagabe und ich sah mir das Ganze genauer an. Die Aussagen ist nämlich nicht ganz korrekt, ohne eine In-Order-Ausgabe ist dies nur in bestimmten Situationen möglich (nämlich wenn der Baum vollständig ist). Doch wieso klappt es nur mit Pre & Post nicht? Hier ein Gegenbeispiel:

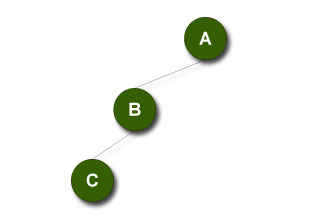
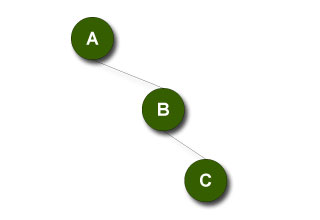
Bei beiden Bäumen ergibt sich als Pre-Order-Durchlauf „A B C“ und als Post-Order „C B A“, obwohl die Binärbäume nicht identisch sind.

Nun ein vollständiger Baum:

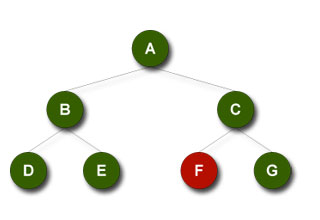
Hier ergeben sich folgende Traversierungen:
Pre-Order: A B D E C F G
Post-Order: D E B F G C A
Hiermit lässt sich der Baum rekursiv rekonstruieren, indem man die Traversierung rückwärts durchspielt und dabei jeweils Teilbäume wiederherstellt.
Wird nun jedoch der rote F-Knoten entfernt (was die Vollständigkeit aufhebt), so ist nur anhand des Pre- und Post-Order-Durchlaufs nicht mehr eindeutig, ob der Knoten G links oder rechts unterhalb des Knotens C sich befindet. Also lassen sich nur vollständige Bäume mit einer Kombination von Pre und Post rekonstruieren.

Bei allen anderen Bäumen ist dies mit einer Kombination eines In-Order-Druchlaufs zusammen mit einem Pre- oder Post-Order-Durchlaufs möglich.

Update: Nach längerer Suche bin ich im Internet noch auf diese Seite gestoßen, die das Problem ebenfalls anspricht und Rekonstruktionen noch genauer untersucht.