IOException.de

Im ersten Teil haben wir zwei einfache Lösungsstrategien entwickelt, wie sich Umkreissuchen der Form “Suche die nächstgelegenen 15 Orte heraus!” durch einen Subquery vorfiltern lassen: Die grundsätzliche Idee ist, über eine Näherungsformel eine Selektion von 15*faktor Datensätzen zu finden, aus denen dann die echt-nächsten Orte bestimmt werden können.

Als Näherung bietet sich so die Pythagorasformel an, die in diesem Beitrag in der simplen Form (Breiten- und Längengerade gehen gleich gewichtet ein) und der verbesserten (mit Gewichtung von 1:1,57 in Deutschland) untersucht wird. Dabei gilt grundsätzlich die Frage zu klären, wie groß in beiden Fällen wohl der faktor gewählt werden muss, damit in den meisten Fällen in der Näherungsselektion auch alle 15 echt-nächsten Orte enthalten sind. Daneben interessiert natürlich, wie groß der Performancegewinn beider Strategien ausfällt.

Dazu habe ich ein kleines Testscript in node.js geschrieben, das eine ganze Reihe Testfälle generiert und durchspielt. Insgesamt wurden für 200 zufällige Orte in Deutschland oder grenznahen Regionen jeweils die 1, 5, 10, 20, 50, 100, 150 und 200 echt-nächsten Orte gesucht. Das Script ermittelt dabei für die beiden Näherungsformeln, wieviele Datensätze durch diese geliefert werden müssen, damit die gesuchten Orte auch wirklich enthalten sind. Ein mögliches Ergebnis wäre also etwa, dass wir über die einfache Pythagorasformel für den Alexanderplatz Berlin mindestens 25 Datensätze erhalten müssten, damit keiner der 15 echt-nächsten fehlte.
Als Datenbasis dient dabei die Vereinsdatenbank von meinem nodeKO-Projekt, die etwa 2600 echte Vereine enthält und somit auch recht praxisnah für diesen Versuch ist.

Die entstandenen 1600 Messdaten und Auswertungen können bei GoogleDocs eingesehen werden. Das Testscript arbeitet so, dass nie zwei Queries gleichzeitig abgesetzt werden, die Zeitmessungen sind also ohne Last.

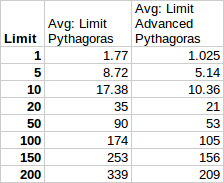Als erstes soll es uns aber gar nicht um die Performance gehen, sondern viel mehr um die Ermittlung eines geeigneten Faktors für die beiden Näherungen. Im Limits-Sheet sind dabei die Messwerte zusammengefasst: Will man z.B. die 20 nächsten Datensätze ermitteln, so sollte man im Mittel über die einfache Pythagorasformel mindestens 35 Datensätze selektieren, bei der verbesserten Formel reichen dagegen 21 (!). Interessant sind auch die Maxima: Nach spätestens 97 Datensätzen waren in allen Testfällen alle 20 gesuchten bei der einfachen Formel enthalten, die verbesserte kam da mit einem maximalen Limit von 30 aus. Im Mittel über alle Tests ergibt sich, dass, wer die Pythagorasformel anwendet, den faktor wenigstens bei 1.75 ansetzen sollte. Bei Hinzunahme des Verhältnisses lon/lat reicht dagegen ein Faktor von 1.05. Wichtig hierbei ist natürlich, dass stets aufgerundet wird.

Der Mittelwert ist aber nur bedingt aussagefähig. Es bleibt immer noch die Frage: Wie häufig ist mein Ergebnis wohl trotzdem falsch, wenn die obigen Werte eingesetzt werden?
Hierfür habe ich die Versuchsergebnisse anders betrachtet: Mit welcher Wahrscheinlichkeit sind alle gesuchten Datensätze wohl enthalten, wenn bei der einfachen Pythagorasformel der Faktor 2 (wir sind mal großzügig…) genutzt wird? Für mich vor allem interessant, weil ich diesen Faktor bei meinem Projekt eingesetzt hatte. Und tatsächlich: Es zeigt sich, dass der Faktor 2 in gerade mal vier von fünf Fällen die gesuchten Ergebnisse liefert. Wer die Pythagoras-Näherung einsetzt, sollte diesen Faktor also doch lieber ein wenig großzügiger bemessen.

Anders ist das bei der verbesserten Pythagorasformel: Mit Faktor 2 hätte sie in allen 200 Testfällen die gesuchten Orte auch mit selektiert. Selbst der Faktor 1.5 ist noch mehr als ausreichend und lieferte in mehr als 99 Prozent die gesuchten Datensätze. Doch wie weit kann man noch runter gehen? Bei einem Faktor von 1.3 sind immer noch sehr annehmbare 98 Prozent der Anfragen korrekt, bei 1.1 fast 97 Prozent.

Und wozu das ganze? – Natürlich um Rechenzeit zu sparen. Die ermittelten Laufzeiten sind leider nur bedingt aussagefähig. Sie geben jeweils an, wieviel Zeit erforderlich war für eben jenen Query, der zuerst alle gesuchten Datensätze enthielt. In Ausnahmefällen kann das also schon mal deutlich mehr sein, als man erhalten würde, wenn man einfach einen fixen Faktor einsetzte. Und dennoch sprechen bereits diese Zahlen für sich: Durch die verbesserte Pythagorasformel erhält man einen Performancegewinn von fast 50 Prozent, die Anwendung lohnt also.

In meinem Projekt äußerte sich der Gewinn sogar noch deutlicher. Dort hatte ich direkt auf meine Tabelle gejoint und gleichzeitig die 15 nächsten Orte gesucht. Resultat: Alle Datensätze wurden erst gejoint und anschließend reduziert. Natürlich ist ein erster möglicher Schritt die Tabelle per Subquery sofort mit der exakten Entfernungsformel zu reduzieren, das bringt auch schon einen deutlichen Gewinn. Noch schneller geht es aber mit den beiden gezeigten Näherungen.
Insbesondere ist es durch die obigen Erkenntnisse möglich, einen Teil der Last auf den Client umzulegen. So wäre ein geeignetes Vorgehen etwa, dem Client stets limit*faktor genäherte Datensätze auf seine Anfrage zurück zu geben, was für den Server sehr viel schneller als die exakte Rechnung ginge. Der Client müsste jetzt selbst den letzten Schritt gehen und für die erhaltenen Orte die exakte Entfernungsberechnung durchführen, um die echt-nächsten limit Orte zu bestimmen.