Posts tagged "tcl" - IOException.de

28 Jul, 2009 von Raimar Wagner 0

Vektorfeldvisualisierung durch Flow Streams

In einem vorherigen Artikel hatte ich bereits über Visualisierungen von Vektorfeldern geschrieben, hier werden wir ein identisches Vektorfeld nutzen. Unser Beispielfeld ist wieder:

$V = x^2*y* e_1 + 2 * x * y^2 * z * e_2 + y* z^3 * e_3$

Wir setzen wieder gridPoints, glyPoints als gegeben vorraus. Des weiteren können wir auch wieder ein Magnituden-Array mag und ein Beschleunigungs-3Tupel-Array velocity als gegeben vorraussetzen:

vtkPoints gridPoints
vtkPoints glyPoints

vtkFloatArray velocity
  velocity SetNumberOfComponents 3
  velocity SetNumberOfValues [expr $x_extend*$y_extend*$z_extend]


vtkFloatArray mag
  mag SetNumberOfComponents 1
  mag SetNumberOfValues [expr $x_extend*$y_extend*$z_extend]

Im nächsten Schritt erzeugen wir wieder aus den Punkten und den zwei Arrays ein strukturiertes Gitter.

vtkStructuredGrid sgrid
  sgrid SetDimensions $x_extend $y_extend $z_extend
  sgrid SetPoints gridPoints
  [sgrid GetPointData] SetVectors velocity
  [sgrid GetPointData] SetScalars mag

Damit wäre die Definition des Feldes abgeschlossen, als erstes müssen die die Streams einen Startpunkt bekommen. In unserem Fall nehmen wir eine Linie auf der die Streams starten sollen.


vtkLineSource rake
  rake SetPoint1 1 9 9
  rake SetPoint2 9 9  9  
  rake SetResolution 200

Der vtkStreamTracer wird im nächsten Schritt die Stromlinien erzeugen die dann mit einem vtkTubeFilter dargestellt werden.

vtkRungeKutta4 integ
vtkStreamTracer streamer
    streamer SetInput sgrid
    streamer SetSourceConnection [rake GetOutputPort]
    streamer SetMaximumPropagation 5000
    streamer SetMaximumPropagationUnitToTimeUnit
    streamer SetInitialIntegrationStep 0.005
    streamer SetInitialIntegrationStepUnitToCellLengthUnit
    streamer SetIntegrationDirectionToBoth
    streamer SetIntegrator integ

vtkTubeFilter streamTube
    streamTube SetInputConnection [streamer GetOutputPort]
    streamTube SetRadius 0.1
    streamTube SetNumberOfSides 12

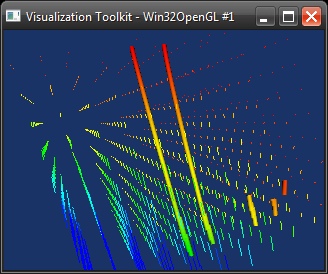
Im letzten Schritt muss nurnoch alles in Mapper und Aktoren gepackt werden (siehe frühere Posts) und wir bekommen das folgende Bild:

flow

3 Jul, 2009 von Raimar Wagner 0

Die VTK Renderpipeline am Beispiel eines Oktaeders

Die VTK Renderpipeline ist im Gegensatz zu traditionellen Grafikpipelines weniger auf Rasterung, Beleuchtung, Clipping, … fokussiert sondern setzt den Schwerpunkt auf das Aufbereiten, Verändern und Repräsentieren von Eingabedaten. Die traditionelle Renderpipeline wird von dem Benutzer soweit wie möglich versteckt. Zu beachten ist dass die Pipeline von der Senke zur Quelle getriggert wird, falls jedoch in einem vorherigen Modul eine Eingabedatenänderung vorgenommen wird, muss für eine aktuelle Darstellung das jeweilige Modul manuell mittels Update getriggert werden.

$\begin{bmatrix} \text{ \textbf{Quelle} } \\ \text{Datenbasis f\$

Dieser Teil der Pipeline bearbeitet und repräsentiert die Eingabedaten. In unserem Fall repräsentieren wir den Oktaeder aus Punkten, Flächen zwischen den Punkten und Farbangaben für jeden Punkt. In den VTK Tcl Bindings sieht das wie folgt aus:

#holds all points
vtkPoints points

points SetNumberOfPoints 6

#insert all points
points InsertPoint 0 1.0 0.0 0.0
#[...]
points InsertPoint 5 0.0 0.0 -1.0

#holds all faces
vtkCellArray polys

polys InsertNextCell 3
   polys InsertCellPoint 0
   polys InsertCellPoint 3
   polys InsertCellPoint 4
#[...]
polys InsertNextCell 3
   polys InsertCellPoint 2
   polys InsertCellPoint 0
   polys InsertCellPoint 5

#set color to i for each face
vtkFloatArray vertexScalars
   for { set i 0 } { $i < 6 } { incr i } {
vertexScalars InsertTuple1 $i $i
}

$\begin{bmatrix} \text{ \textbf{Quelle} } \\ \text{Datenbasis f\$

In unserem Fall besteht der Filter daraus dass alle Eingabedaten (Punkte, Flächen, …) zusammengesetzt werden müssen.

vtkPolyData octahedron
   octahedron SetPoints points
   octahedron SetPolys polys
   [octahedron GetPointData] SetScalars vertexScalars

$\begin{bmatrix} \text{ \textbf{Filter} } \\ \text{Daten- und Datenstrommodifikation} \end{bmatrix} \rightarrow\begin{bmatrix} \text{ \textbf{Mapper} } \\ \text{Erzeugen der Grafikobjekte} \end{bmatrix}$

Im Mapper wird die eigentlich Repräsentation erzeugt, in unserem Fall ist nurnoch eine Bereichsangabe für die Skalare notwendig.

vtkPolyDataMapper octahedronMapper
   octahedronMapper SetInput octahedron
   octahedronMapper SetScalarRange 0 7

$\begin{bmatrix} \text{ \textbf{Mapper} } \\ \text{Erzeugen der Grafikobjekte} \end{bmatrix} \rightarrow \begin{bmatrix} \text{ \textbf{Actor} } \\ \text{Repr\$

Im Actor werden die Parameter der Datenrepräsentation spezifiziert, meist sind das klassische Computergraphikparameter wie Beleuchtung, Transparenz, …

vtkActor octahedronActor
   octahedronActor SetMapper octahedronMapper

$\begin{bmatrix} \text{ \textbf{Actor} } \\ \text{Repraesentationsparameter} \end{bmatrix} \rightarrow \begin{bmatrix} \text{ \textbf{Renderer \&Fenster} } \\ \text{Zeigt alle Actoren an} \end{bmatrix}$

In diesem Teil werden alle Actors einen Renderer zugewiesen und über ein Fenster gezeichnet.

vtkRenderer ren1 
   ren1 AddActor octahedronActor
   ren1 SetBackground 0.1 0.2 0.4

vtkRenderWindow renWin
   renWin AddRenderer ren1
   renWin SetSize 300 300

vtkRenderWindowInteractor iren
   iren SetRenderWindow renWin

vtkInteractorStyleTrackballCamera style
   iren SetInteractorStyle style

iren AddObserver UserEvent {wm deiconify .vtkInteract}

iren Initialize

wm withdraw .

Die Interaktionskomponenten die noch initialisiert werden sind nicht direkt Teil der Pipeline sondern nebenläufige Module.

Die komplette VTK Pipeline sieht am Ende wie folgt aus:

$\begin{bmatrix} \text{ \textbf{Quelle} } \end{bmatrix} \rightarrow \begin{bmatrix} \text{ \textbf{Filter} } \end{bmatrix} \rightarrow \begin{bmatrix} \text{ \textbf{Mapper} } \end{bmatrix} \rightarrow \begin{bmatrix} \text{ \textbf{Actor} } \end{bmatrix} \rightarrow \begin{bmatrix} \text{ \textbf{Renderer \& Fenster} } \end{bmatrix}$

und das Ergebnis in den Tcl Bindings:

okt

23 Jun, 2009 von Raimar Wagner 0

Videoexport aus VTK mittels vtkAVIWriter

Um eine interessante Animation in VTK als Video zu exportieren bietet sich der vtkAVIWriter an. Dieser Filter kann Animation als .avi Datei rausschreiben. Wieder kommt hier VTK in den Tcl Bindings zum Einsatz, die Übertragung auf andere Bindings sollte aber 1:1 möglich sein. An das Ende der Filterkette hängen wir mit dem vtkWindowToImageFilter, einen Filter der das Bild eines vtkRenderWindow aus der momentanen Fensterdarstellung extrahiert.

vtkRenderWindow renderW

#[ ... ]

vtkWindowToImageFilter imageF
  imageF SetInput renderW

Im nächsten Schritt kommt der vtkAVIWriter zum Einsatz, nach der Initialisierung wird nach jedem Frame die Filterkette aktualisiert und der aktuelle Frame rausgeschrieben. Nach dem letzten Frame wird der vtkAVIWriter gestoppt.

vtkAVIWriter aviW
  aviW SetFileName "animation.avi"
  aviW SetInputConnection [imageF GetOutputPort]
  aviW Start

for {set k 0} {$k<$frames} {incr k} {
   
  #do computation
   
  #render window
  renderW Render
  #call modified at filter
  imageF Modified
  #write frame
  aviW Write

}
#end of animation
aviW End

Für ein Beispiel siehe “Visualisierung von Winkelgeschwindigkeiten in Vektorfeldern”.

21 Jun, 2009 von Raimar Wagner 1

Visualisierung von Winkelgeschwindigkeiten in Vektorfeldern

Um für ein gegebenes Beschleunigungsfeld die Winkelgeschwindigkeiten zu visualisieren bietet es sich an, an äquidistant gestreuten Stützstellen Würfel zu visualisieren die um die Beschleunigungsachse rotiert. Ein mögliches Beispielfeld ist:

$V = x^2*y* e_1 + 2 * x * y^2 * z * e_2 + y* z^3 * e_3$

Für die Umsetzung wurde VTK mit den Tcl Bindings verwendet. Zu Beginn benötigen wir zwei vtkPoints, eines für die geglyphten Würfel und eins für die eigentlichen Punkte im Raum. Im folgenden können wir gridPoints, glyPoints als gegeben vorraussetzen. Des weiteren können wir ein Magnituden-Array mag und ein Beschleunigungs-3Tupel-Array velocity als gegeben vorraussetzen:

vtkPoints gridPoints
vtkPoints glyPoints

vtkFloatArray velocity
  velocity SetNumberOfComponents 3
  velocity SetNumberOfValues [expr $x_extend*$y_extend*$z_extend]


vtkFloatArray mag
  mag SetNumberOfComponents 1
  mag SetNumberOfValues [expr $x_extend*$y_extend*$z_extend]

Im nächsten Schritt müssen die Würfel Glyphs initialisiert werden und zu jedem cube_$i ein Mapper und Filter definiert werden.

#iterate thru all glyph points
for {set i 0} {$i < [eval glyPoints GetNumberOfPoints]} {incr i} {  
  
  #create cubes
  vtkCubeSource cube_$i
    set pt [glyPoints GetPoint $i]
    
  #get nearest pnt
  set ref [eval loc FindClosestPoint [lindex $pt 0] [lindex $pt 1] [lindex $pt 2] ] 
  set vl [velocity GetTuple3 $ref]
      
      
  #turn and translate
  vtkTransform cubeTransform_$i
    cubeTransform_$i PostMultiply
    cubeTransform_$i Translate 0 0 0
    set n [eval norm [lindex $vl 0] [lindex $vl 1] [lindex $vl 2]]
    cubeTransform_$i RotateWXYZ $n [lindex $vl 0] [lindex $vl 1] [lindex $vl 2]
    cubeTransform_$i Translate [lindex $pt 0] [lindex $pt 1] [lindex $pt 2]
  
  #create filter for transformation
  vtkTransformPolyDataFilter cubeTransformFilter_$i
    cubeTransformFilter_$i SetInput [cube_$i GetOutput ]
    cubeTransformFilter_$i SetTransform cubeTransform_$i
  
  #create mapper
  vtkPolyDataMapper   cubeMapper_$i
      cubeMapper_$i SetInput [cubeTransformFilter_$i GetOutput]
}

Im letzten Schritt folgt die Animation mit der Kameradrehung.

#render 900 frames
for {set k 0} {$k<900} {incr k} {
    
    
  #rotate all glyphs    
  for {set i 0} {$i<[eval glyPoints GetNumberOfPoints]} {incr i} {
    set pt [glyPoints GetPoint $i]
    
    #find velocity to point
    set ref [eval loc FindClosestPoint [lindex $pt 0] [lindex $pt 1] [lindex $pt 2] ] 
    set vl [velocity GetTuple3 $ref]
    
    #transform every cube
    cubeTransform_$i Identity
    cubeTransform_$i Translate 0 0 0
  
    set n [eval norm [lindex $vl 0] [lindex $vl 1] [lindex $vl 2]]
    cubeTransform_$i RotateWXYZ [expr $k * $n/1000] [lindex $vl 0] [lindex $vl 1] [lindex $vl 2]
    cubeTransform_$i Translate [lindex $pt 0] [lindex $pt 1] [lindex $pt 2]
  
  
  }

  #move camera & render frame
  [ren1 GetActiveCamera] Azimuth 0.1
  renWin Render
 
}

Mit zusätzlicher Einblendung der Beschleunigungvektoren sieht das Ergebnis dann so aus: