30 Aug, 2011 von Benjamin Erb 3
Einfache Visualisierung von Geodaten – Teil 2: Leaflet & jquery.couch.js
Im vorherigen Teil haben wir gesehen, wie man Geodaten mithilfe von CouchDB abspeichern kann. Da diese Datenbank zugleich ein Webserver ist und die Daten im JSON-Format gespeichert werden, eignet sie CouchDB auch gut für AJAX-Abfragen. Hierfür gibt es eine auf jQuery aufbauende Library namens jquery.couch.js, die von den AJAX-Requests abstrahiert und direkt browser-seitige Interaktionen mit der Datenbank ermöglicht.
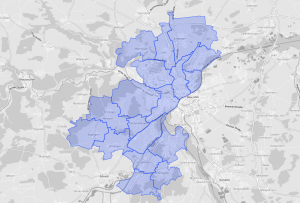
Im diesem Beitrag soll gezeigt werden, wie man mit der offenen Karten-Library Leaflet und jquery.couch.js geographische Daten aus CouchDB heraus auf einer Karten anzeigen kann.
Beispiel-Visualisierung von ulmapi.de, ebenfalls basierend auf CouchDB und Leaflet.
Wir verwenden die CouchApp aus dem ersten Teil weiter, und fügen zu den bisherigen Map/Reduce Views noch statische HTML- und Javascript-Dateien hinzu (im _attachments Ordner), die dann im Browser abgerufen werden können. Beim Aufruf dieser Webseite wird ein HTML-Grundgerüst übertragen, sowie eine JavaScript-Datei, die beim Aufruf die eigentlichen Datensätze via jquery.couch.js aus der CouchDB nachlädt.
Als Mapping-Library verwenden wir Leaflet, eine Open-Source Bibliothek für Kartendarstellungen im Browser. Leaflet abstrahiert von verschiedenen Kartenprovidern und erlaubt es somit, unterschiedliche Datenquellen zu verwenden, wie zum Beispiel auch Bing Maps oder Cloudmade. Letzteres ist ein Service, der auf Basis der Open Street Map Daten Kartenkacheln mit individuellen Stilen rendert und hostet – für Visualisierungen oft sehr hilfreich, da reguläre Karten meist zu viele Karteninformationen enthalten oder farblich überladen sind. In unserem Fall haben wir einen einfach Graustufenkarte gewählt. Leaflet selbst lässt sich relativ leicht verwenden, es muss eine CSS-Datei sowie eine JavaScript-Datei importiert werden, und ein div-Block im HTML enthalten sein, worin später die Karte gerendert werden soll. Somit sieht unser HTML-Gerüst zu Beginn so aus:
<!doctype html> <html> <head> <link rel="stylesheet" href="style/leaflet.css" /> <script type="text/javascript" src="js/jquery.min.js"></script> <script type="text/javascript" src="js/jquery.couch.js"></script> <script type="text/javascript" src="js/leaflet.js"></script> <script type="text/javascript" src="js/maploader.js"></script> </head> <body> <div id="map"></div> </body> </html>
Es werden jQuery, jquery.couch.js und die Leaflet-Libs geladen, und die letzte importierte JavaScript-Datei soll nun unseren Code zum initialisieren der Karte und dem Laden der Daten aus der CouchDB enthalten. Zunächst erstellen wir eine Karte und rendern sie, sobald die Seite vollständig geladen wurde (jQuery Callback für document.ready):
$(document).ready(function(){
var cloudmadeUrl = 'http://{s}.tile.cloudmade.com/[YOUR_API_KEY]/33481/256/{z}/{x}/{y}.png';
var cloudmadeAttribution = 'UlmApi.de / Shape Files: Stadt Ulm (cc-by-sa), Map data © 2011 OpenStreetMap contributors, Imagery © 2011 CloudMade';
var cloudmade = new L.TileLayer(
cloudmadeUrl, {
maxZoom : 18,
attribution : cloudmadeAttribution
});
var map = new L.Map('map', {
center : new L.LatLng(48.399976,9.995399),
zoom : 12,
layers : [ cloudmade ],
zoomControl : false
});
});
In der cloudmadeUrl muss für Cloudmade Karte ein korrekter API-Key angegeben werden, der nächste Parameter im Pfad identifiziert den Kartentyp. Beim Initialisieren der Karte wird dann die ID des divs angeben, bei uns ‘map’. Nun sollte unsere Karte bereits dargestellt werden, nachdem wir die CouchApp neu deployen (außerhalb des Fokus dieses Artikels, mehr dazu auf couchapp.org).
Was nun noch fehlt, ist das Nachladen der Geodaten aus der CouchDB und die Anzeige auf der Karte. Hierfür verwenden wir jquery.couch.js als Wrapper für die AJAX-Requests gegen CouchDB und die GeoJSON-Funktionalität von Leaflet:
$.couch.db('database_name').view('design_doc_name/view_name', {
success: function(data){
if(data && data.rows && data.rows.length){
var geoJsonLayer = new L.GeoJSON();
for(var i = 0;i<data.rows.length;i++){
geoJsonLayer.addGeoJSON(data.rows[i].value.geometry);
}
map.addLayer(geoJsonLayer);
}
}
});
Das obige Snippet sollte im vorherigen Code hinter der Erzeugung der Karte eingefügt werden. Es ruft von der Datenbank ‘database_name’ den View ‘view_name’ des Design-Dokuments ‘design_doc_name’ auf, und iteriert bei erfolgreicher Abfrage über alle Zeilen. Von jeder Zeile wird dabei die geometry-Property zu einem GeoJSON-Layer hinzugefügt, der am Ende an die Karte übergeben wird. Da unser View aus Teil 1 bereits GeoJSON generiert, und Leaflet nativ GeoJSON lesen und darstellen kann, ist das Hinzufügen von Geodaten auf die Karte sehr einfach.
Hier noch ein paar weiterführende Links mit vertiefenden Inhalten zu den einzelnen Themen:
- Leaflet Reference
- CouchApp
- Diplomarbeit von Lena Herrmann über Webanwendungen mit CouchDB und CouchApp
![\begin{bmatrix} \text{ \textbf{Quelle} } \\ \text{Datenbasis f\](http://l.wordpress.com/latex.php?latex=%20%5Cbegin%7Bbmatrix%7D%20%5Ctext%7B%20%5Ctextbf%7BQuelle%7D%20%7D%20%20%5C%5C%20%5Ctext%7BDatenbasis%20f%5C%22%7Bu%7Dr%20die%20Visualisierung%7D%20%20%5Cend%7Bbmatrix%7D%20&bg=FFFFFF&fg=000000&s=0 "\begin{bmatrix} \text{ \textbf{Quelle} } \\ \text{Datenbasis f\")
![\begin{bmatrix} \text{ \textbf{Quelle} } \\ \text{Datenbasis f\](http://l.wordpress.com/latex.php?latex=%20%5Cbegin%7Bbmatrix%7D%20%5Ctext%7B%20%5Ctextbf%7BQuelle%7D%20%7D%20%20%5C%5C%20%5Ctext%7BDatenbasis%20f%5C%22%7Bu%7Dr%20die%20Visualisierung%7D%20%20%5Cend%7Bbmatrix%7D%20%5Crightarrow%20%20%5Cbegin%7Bbmatrix%7D%20%5Ctext%7B%20%5Ctextbf%7BFilter%7D%20%7D%20%20%5C%5C%20%5Ctext%7BDaten-%20und%20Datenstrommodifikation%7D%20%20%5Cend%7Bbmatrix%7D%20&bg=FFFFFF&fg=000000&s=0 "\begin{bmatrix} \text{ \textbf{Quelle} } \\ \text{Datenbasis f\")
![\begin{bmatrix} \text{ \textbf{Mapper} } \\ \text{Erzeugen der Grafikobjekte} \end{bmatrix} \rightarrow \begin{bmatrix} \text{ \textbf{Actor} } \\ \text{Repr\](http://l.wordpress.com/latex.php?latex=%20%5Cbegin%7Bbmatrix%7D%20%5Ctext%7B%20%5Ctextbf%7BMapper%7D%20%7D%20%20%5C%5C%20%5Ctext%7BErzeugen%20der%20Grafikobjekte%7D%20%20%5Cend%7Bbmatrix%7D%20%5Crightarrow%20%20%5Cbegin%7Bbmatrix%7D%20%5Ctext%7B%20%5Ctextbf%7BActor%7D%20%7D%20%20%5C%5C%20%5Ctext%7BRepr%5C%22%7Ba%7Dsentationsparameter%7D%20%20%5Cend%7Bbmatrix%7D%20&bg=FFFFFF&fg=000000&s=0 "\begin{bmatrix} \text{ \textbf{Mapper} } \\ \text{Erzeugen der Grafikobjekte} \end{bmatrix} \rightarrow \begin{bmatrix} \text{ \textbf{Actor} } \\ \text{Repr\")
